Camera Technology Overview

To correctly interpret an image, you need to understand how it has been formed in the first place.

If your camera is set up poorly or the optics or the image sensor does not fit the scene you want to capture, even the best computer vision algorithm will not help you. Also, when you get to the point where you will reconstruct a scene in 3D space, you will need to have a solid knowledge of camera geometry and on the various coordinate systems involved.

Outlines

• Pinhole Camera The most basic model

• Lenses Key component of camera systems which of its properties influence image appearance and quality and which parameters you have to consider in order to successfully extract meaningful information from these images

The Pinhole camera

A very simple camera can be designed by placing a light barrier with a tiny opening (the pinhole) between an object of interest. The light emitted by the object passes through the pinhole and lands on a photosensitive surface which stores the light information as an image. The reason why the pinhole has been made so small is to avoid image blurring due to superimposing rays of light stemming from various parts of the object of interest.

This simple principle has been well known for centuries and was for example used by artists to create photo-realistic portraits.

A formal model of the pinhole camera model is shown below.

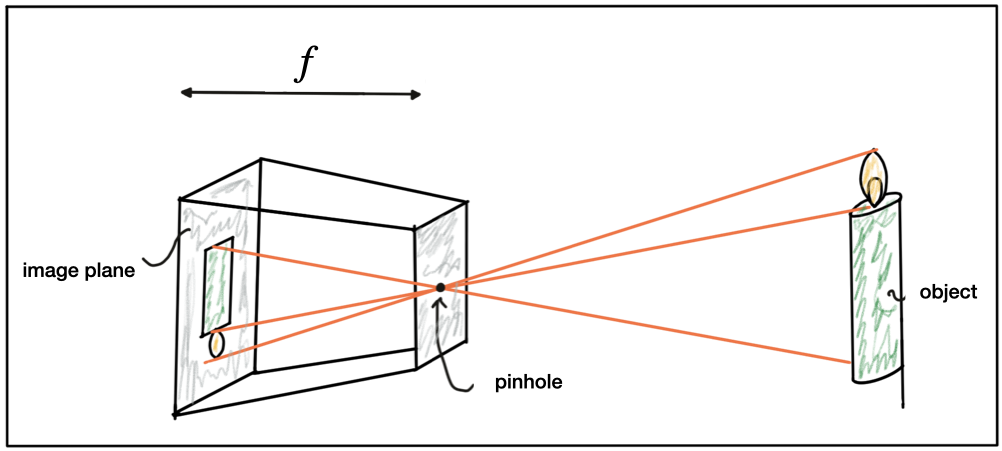
The photosensitive surface on the left is called the image plane whereas the pinhole is called the camera center. The distance between the camera center and the image plane is called the focal length f.

A point P on the object of interest can be mapped to a point P’ on the image plane by casting a beam through the center of projection until it hits the image plane as shown in the figure below.

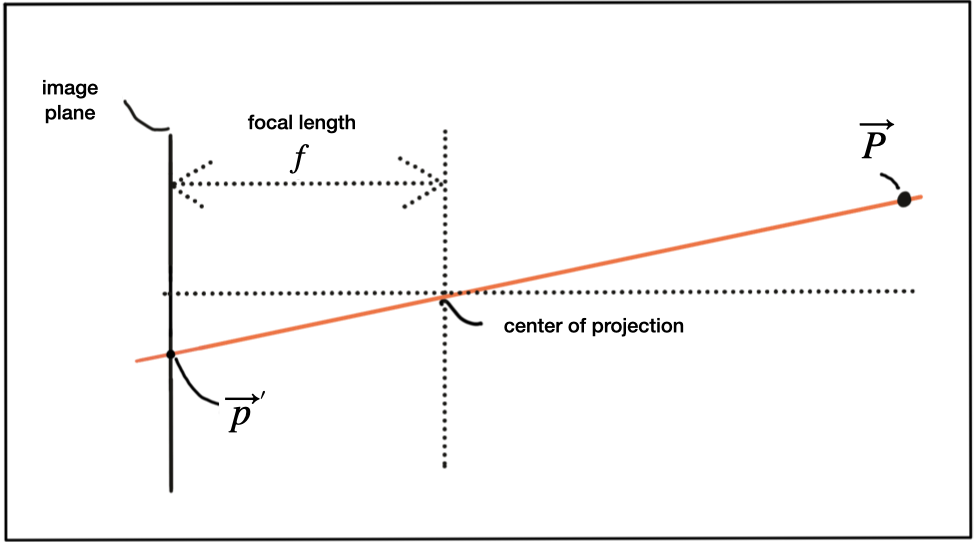
In three-dimensional space, the relation between P and P' is expressed by the following equations:

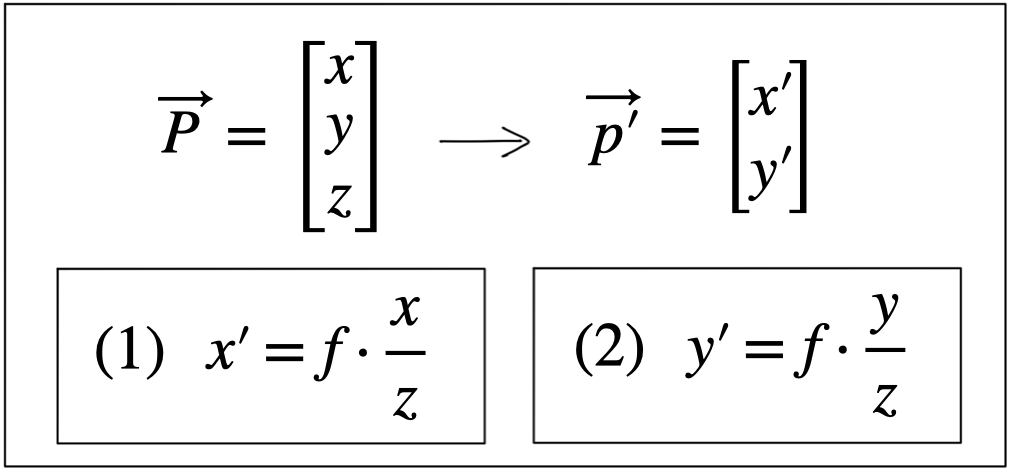
Based on these equations, we are able to compute the 2D position of an object on the image plane, given the 3D position of the object in space as well as the focal length of the camera. Note however that the resulting coordinates x’ and y’ are metrical coordinates and not pixel positions yet.

The problem with pinhole cameras is that the amount of light passing through the pinhole is not sufficient to generate a decent image on an image sensor. If one were to increase the amount of light by widening the pinhole opening as shown in the figure below, rays of light from other parts of the object of interest would superimpose each other, leading to a blurring effect: The larger the pinhole, the brighter the image but at the same time, the more severe the blurring of the object on the image plane would be.

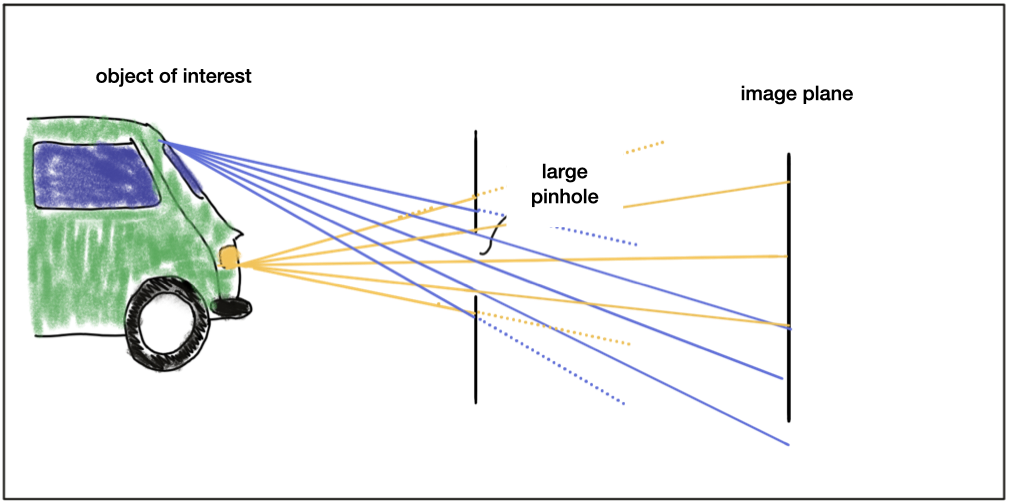
One way to solve this problem is use a lens, which is able to capture multiple rays of light that emanate from the same point on the object of interest.

Lenses and Aperture

A properly sized and positioned lens refracts all rays of light that emanate from a point P1 on an object in space such that they converge to a single point p_1'p1′ in the image plane. Rays of light passing through the lens center are not refracted however, they continue on as a straight line until they intersect the image plane.

Points on the object that are closer or farther away, such as P_2P2, appear out of focus on the image plane, because the set of light rays emanating from them does not converge in a point but rather in a circle with a finite radius instead. This blurry circle is usually referred to as circle of confusion (COF). To reduce blurring, an aperture can be used, which is a concentric opening of usually adjustable size placed directly behind the lens. The following figure illustrates the principle:

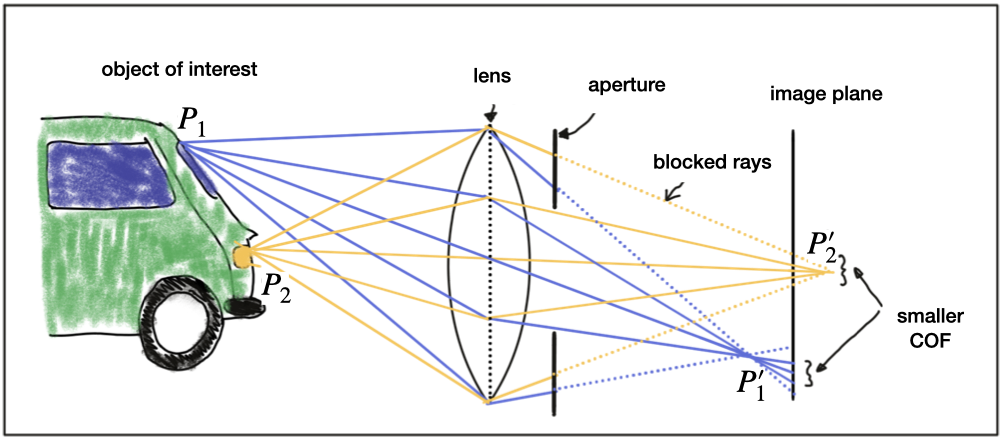
By reducing the diameter of the aperture, light rays passing through the lens on the outer edges are blocked, which reduces the size of the COF on the image plane. It can easily be seen that a smaller aperture results in reduced blurring, but at the expense of low light sensitivity. The larger the aperture, the more light rays are focused onto the image area, resulting in brighter images with a better signal-to-noise ratio.

So how can we compute where an object in space will appear in the image? Given a 3D point in space, its 2D position on the image plane after passing through a lens can be computed similar to the pinhole camera. In practice, lenses introduce distortion into images, depending on the lens type. The distortion most relevant to practice is called “radial distortion”. It is caused by the focal length of the lens not being uniform over its diameter. Therefore, the magnification effect of the lens changes depending on the distance between the camera center (the optical axis) and the ray of light passing through the lens. If the magnification increases, the resulting distortion effect is called pin cushion distortion. If it decreases, it is called barrel distortion instead. Barrel distortions usually occur, when wide-angle lenses are used. In the figure below, both distortion types are illustrated.

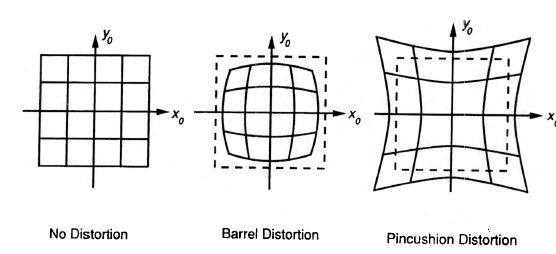
When extracting information from camera images, many applications seek to draw conclusions on the spatial location of objects of interest (e.g. vehicles). To get there, the distortion effect of the lens must be removed or at least mitigated. The relevant process is called calibration. For each camera-lens-setup, a calibration procedure must be performed so the distortion parameters can be individually computed.

This is usually done by taking a set of pictures of well-known objects such as planar checkerboard patterns, from whose known geometry all lens and image sensor parameters can be robustly derived. The process of removing distortions from a camera image is called rectification. In the image below, the calibration setup used to rectify most of the images in this course is shown. It can easily be seen that lines at both left and right are distorted significantly.

It is beyond the scope of this course however to go into the details of distortion correction. Most of the images you will be using are already free of lens distortion. When using your own camera setup however, a calibration procedure must be performed when precise measurements and a spatial reconstruction of objects is the goal.

As mentioned before, the projection of points in 3D space onto the image plane does not directly correspond to what we see in actual digital images, which are made up of thousands of picture elements or pixels. To understand how images can be expressed in discrete pixels, we need to take a closer look at the above-mentioned camera model once more.

In the figure below, the camera center is shown with a position O in space along with its own coordinate system with axes i, j and k, where k is pointing into the direction of the image plane. The position C′ where k intersects the image plane is called the principal point and represents the center of the image coordinate system.The first step after projecting a point PP in space onto the image plane is thus to subtract the principal point coordinates so that the discrete image has its own coordinate system centered in e.g. the lower left corner of the image plane.

Note that the indices of spatial coordinates sometimes differ depending on the area of application and on the author you are reading. In computer vision, points in space are often described with i, j and k or with X, Y and Z. When referring to points on the image plane though, in almost all cases, the coordinate axes are denoted as x and y.

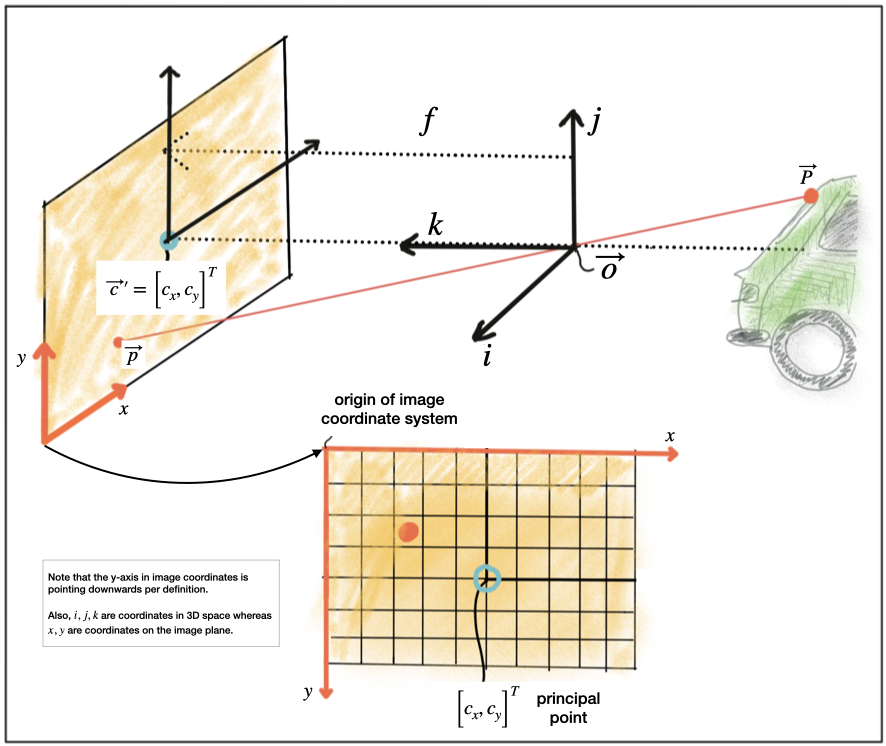
The second step in the transformation process is to move from metric to pixel coordinates. To do so, we can use parameters kk and ll provided by the calibration procedure which convert meters to pixels and which can be easily integrated into the projection equations as seen below. Note that in image coordinates, the y-axis has its origin in the upper-left corner and is pointing downwards.

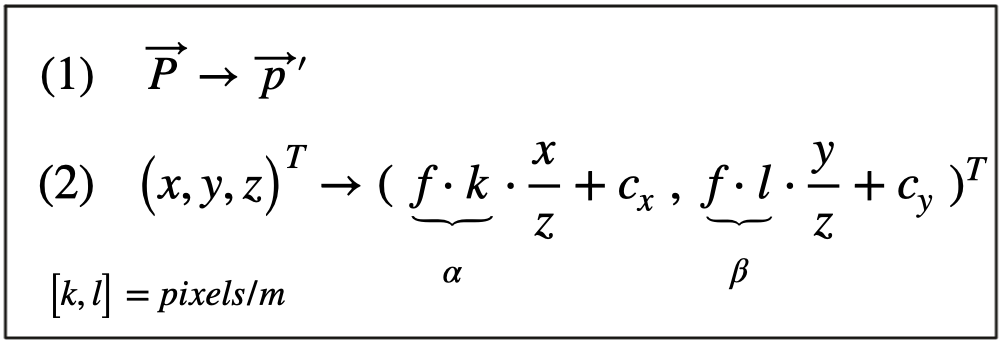
In a later section of this course, we will be mapping Lidar 3D points into the camera image. To do so, we will make use of these equations. Specifically, the product of focal width ff and kk and ll respectively (also termed alpha and beta) will be used in a calibration matrix to simplify the mapping operation significantly.

One final note on image rectification: In many applications (e.g. feature tracking) it makes sense to process the original image to avoid interpolation errors when the rectified image is computed and transformed pixels do not fall exactly onto the center of a discrete pixel in the rectified image but close to the border to another pixel instead. In such a case, it is advisable to locate the features in the unmodified original image and then transform the resulting coordinates using the equations above. When using deep learning based on a set of trained weights, it makes sense to rectify the image first before feeding it to a network - if we would use the original image, distortions (such as from a fish-eye lens) would lead to detection errors as networks are usually trained on a distortion-free image set.

Imagers and Bayer Pattern

How rays of light with a certain wavelength are converted into color pixels that can be stored digitally 😉

When an image is captured by a camera, light passes through the lens and falls on the image sensor. This sensor consists of light sensitive elements that register the amount of light that falls on them and convert it into a corresponding number of electrons. The more light, the more electrons are generated. Once the exposure time is complete, the generated electrons are converted into a voltage, which is finally transformed into a discrete number by means of an A/D-converter.

Currently, there are two main image technologies, which are CCD (Charge-Coupled Device) and CMOS (Complementary Metal-oxide Semiconductor). Both technologies convert electrons into voltage and are inherently color blind, as they can not distinguish the different wavelengths which generate the electrons.

To enable color vision, tiny filter elements (also micro-lenses) are placed in front of each pixel which only allow a certain wavelength to pass through. One common way to map wavelength to color is to arrange the filter elements in an RGB (Red, Green, Blue) pattern to allow the primary colors to pass through individually, which gives us three individual images - one for each primary color.

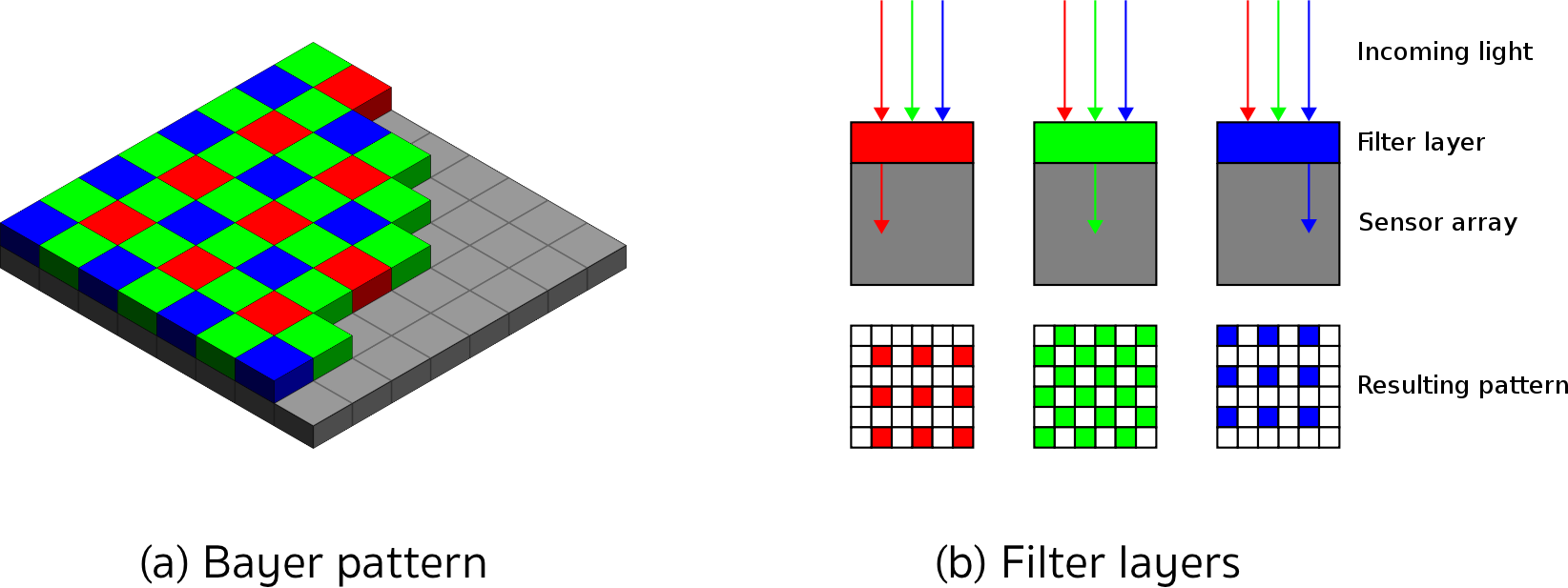
Mixed in different combinations, RGB values can produce most of the colors visible to the human eye. When each discrete color value is coded with 8-bits (i.e. 256 values), a total of 16.7 million different colors can be created with the RGB filter concept. The most common way of arranging the RGB filters is called a Bayer pattern, which has alternating rows of red-green and green-blue filters. Since the human eye is more sensitive to green than to red or blue, the Bayer array has twice as many green color filters. When processing color images in a computer vision application, all three RGB layers are available and it has to be decided which color layers to use. If processing power is limited, the different channels are combined into a gray scale image. In the upcoming section on computer vision, you will be introduced to the OpenCV computer vision library. You can take a look at the conversion formula to get from RGB to grayscale which is used in the method cvtColor here:

OpenCV: Color conversions

The output RGB components of a pixel are interpolated from 1, 2, or 4 neighbors of the pixel having the same color. There are several modifications of the above pattern that can be achieved by shifting the pattern one pixel left and/or one pixel up.

https://docs.opencv.org/3.1.0/de/d25/imgproc_color_conversions.html

CCD vs. CMOS

In a CCD sensor, the electrons collected in each picture element are transferred from the chip through a single or only a few output nodes. The charges are then converted to voltage levels, buffered, and sent out as an analog signal. This signal is then amplified and converted to discrete numbers using an A/D-converter outside the sensor. Originally, CCD technology has had several advantages compared to CMOS, such as higher light sensitivity and less noise. In recent years, however, these differences have all but disappeared. The major disadvantages of CCD are a higher production price and a higher power consumption (up to 100x more than CMOS) , which usually leads to heat issues in the camera.

CMOS sensors were originally used for machine vision applications, but the image quality was poor due to their inferior light sensitivity. With modern CMOS sensors however, both quality and light sensitivity have significantly increased. The CMOS technology has several advantages: Unlike CCD, CMOS chips incorporate amplifiers and A/D-converters, which brings a huge cost advantage. With CCD, those components are located outside of the chip. CMOS sensors also have a faster data readout, lower power consumption, higher noise immunity, and a smaller system size. In automotive applications, almost all cameras use CMOS sensors because of these advantages. The camera setup used for recording most of the image sequences in this course can be found here:

The KITTI Vision Benchmark Suite

This page provides additional information about the recording platform and sensor setup we have used to record this dataset. Our recording platform is a Volkswagen Passat B6, which has been modified with actuators for the pedals (acceleration and brake) and the steering wheel.

http://www.cvlibs.net/datasets/kitti/setup.php

Types of Lenses used in Self-driving Cars

• Wide angle lenses: for near field

• Narrow angle lenses: for far field

One important factor is to have intense light sensitivity, requires large aperture to get as much light in as possible.

Types of Chips sets used in Cameras

The regular smartphone chip has a typical RGB bio pattern and has maybe a resolution of 16 megapixels. The resolution for self-driving cars is not that important, it is really about the sensitivity. Self-driving cars use chips ranging from 1 megapixel to 8 megapixels in terms of resolution. There are also chips that don't have that regular RGB bio pattern but a clear pixel -every fourth pixel has no color filter-, so you can have better light sensitivity because of that.

What makes a Camera Automotive Grade

1. Packaging

2. Ruggedness

3. Durability of the entire setup (integration of the chip and the lens, so it doesn't decalibrate quickly with varying temperatures in different conditions)

4. They have larger pixels than normal cameras to allow more photons to fall into the one pixel, so you have better low light resolution.

Notes

• The focal length is the distance between the center of the camera and its focus point.

• There are a couple of ways that blurring of objects in an image can be reduced:

1. By introducing an aperture to reduce the diameter of the circle of confusion.

2. By moving the camera (or object) to a position such that the focus points of all rays emanating from the object are on the image plane.

• The principal point is the coordinate on the image plane where the optical axis of the camera intersects the image plane. In order to compute the pixel position of a point projected onto the image plane, the principal point location is used to shift the image coordinate system to the lower (or upper) left corner of the image plane.

• The Bayer pattern uses twice as many green pixels as the human (daylight) vision is more sensitive to green light.

Does it make sense to have multiple cameras on self-driving car?

It makes a lot of sense because you have different use cases. You want to have different field of views. For tailor lens, you want to see further away. You have wide angle lenses for near field around the car.

You have different chips that cover different spectrum, for night time driving, for high dynamic range. There are various types of applications and there are specialized cameras for each of those fields.

How reliable is camera only depth detection?

Camera only depth perception can be very reliable mostly in the near field, in the far field it is getting really difficult.

How to stitch together images from different cameras on the same vehicle?

We don't do relative synchronization or stitching of images, but for each camera we do absolute calibration with respect to a common time frame or common position that is usually the rear axle of the vehicle for instance. If we have this intrinsic and extrinsic calibrations, we can map everything into one holistic global frame.

Camera downsides

Measuring distance very precisely in the far field, because of the high resolution in a radial direction, you can see cross traffic really well -considering a front facing camera- and measure the velocity, but if you have oncoming traffic it is really difficult to detect that velocity accurately.