Clustering Obstacles
You have a way to segment points and recognize which ones represent obstacles for your car. It would be great to break up and group those obstacle points, especially if you want to do multiple object tracking with cars, pedestrians, and bicyclists, for instance. One way to do that grouping and cluster point cloud data is called euclidean clustering.
Euclidean Clustering
The idea is you associate groups of points by how close together they are. To do a nearest neighbor search efficiently, you use a KD-Tree data structure which, on average, speeds up your look up time from O(n) to O(log(n)). This is because the tree allows you to better break up your search space. By grouping points into regions in a KD-Tree, you can avoid calculating distance for possibly thousands of points just because you know they are not even considered in a close enough region.
Euclidean Clustering Arguments
- The euclidean clustering object
ectakes in a distance tolerance. Any points within that distance will be grouped together. It also has min and max arguments for the number of points to represent as clusters. The idea is: if a cluster is really small, it’s probably just noise and we are not concerned with it. Also a max number of points allows us to better break up very large clusters. If a cluster is very large it might just be that many other clusters are overlapping, and a max tolerance can help us better resolve the object detections. The last argument to the euclidean cluster object is the Kd-Tree. The tree is created and built using the input cloud points, which in this case are going to be the obstacle cloud points.
- The number of points for each cluster can be logged. This can be a helpful debugging tool later when trying to pick good min and max point values.
- Some time and effort will be needed to pick good hyperparameters, but many cases actually there won't be a perfect combination to always get perfect results.
Implementing KD-Tree
- A KD-Tree is a binary tree that splits points between alternating axes. By separating space by splitting regions, nearest neighbor search can be made much faster when using an algorithm like euclidean clustering.
- A 2D point represented by a vector containing two floats, and a point ID. The ID is a way to uniquely identify points and a way to tell which index the point is referenced from on the overall point cloud.
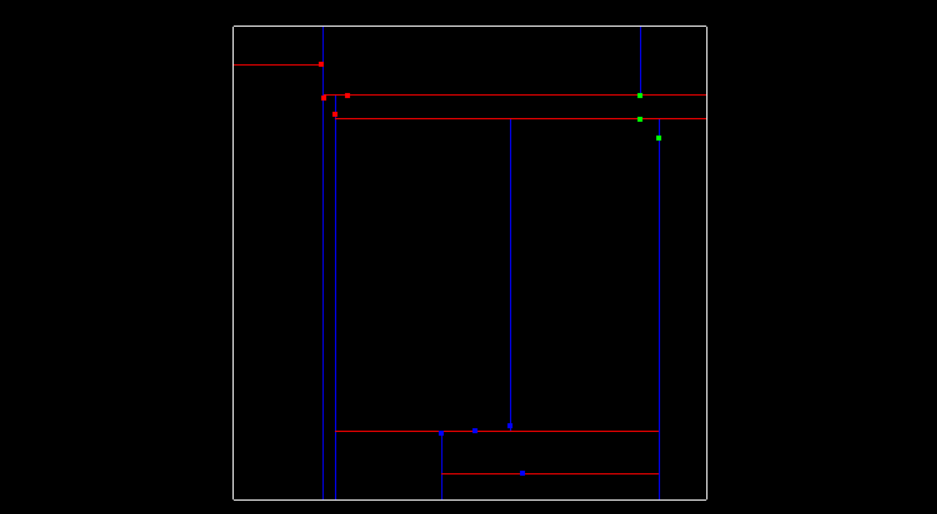
- The image below shows line separations, with blue lines splitting x regions and red lines splitting y regions. The image shows what the tree looks like after all 11 points have been inserted.
Now let’s talk about how exactly the tree is created.
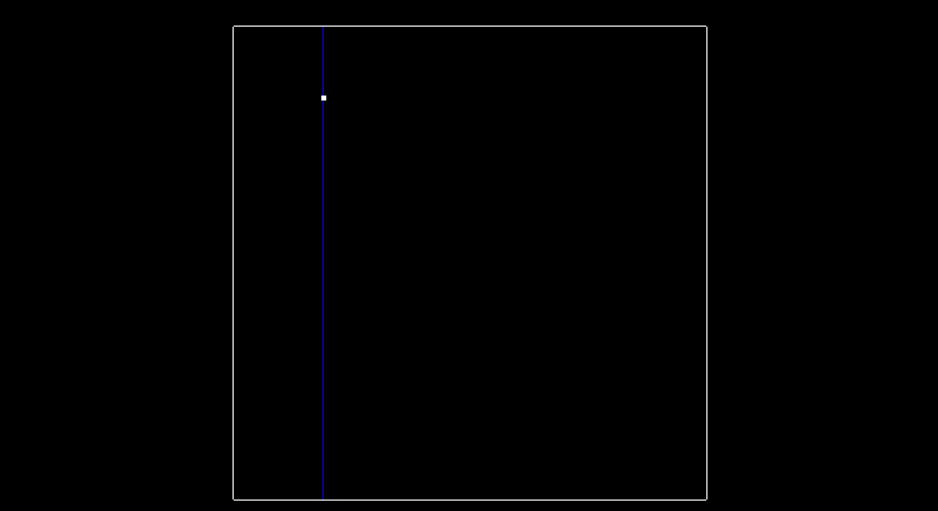
At the very beginning when the tree is empty, root is NULL. The point inserted becomes the root, and splits the x region. Here is what this visually looks like, after inserting the first point (-6.2, 7).
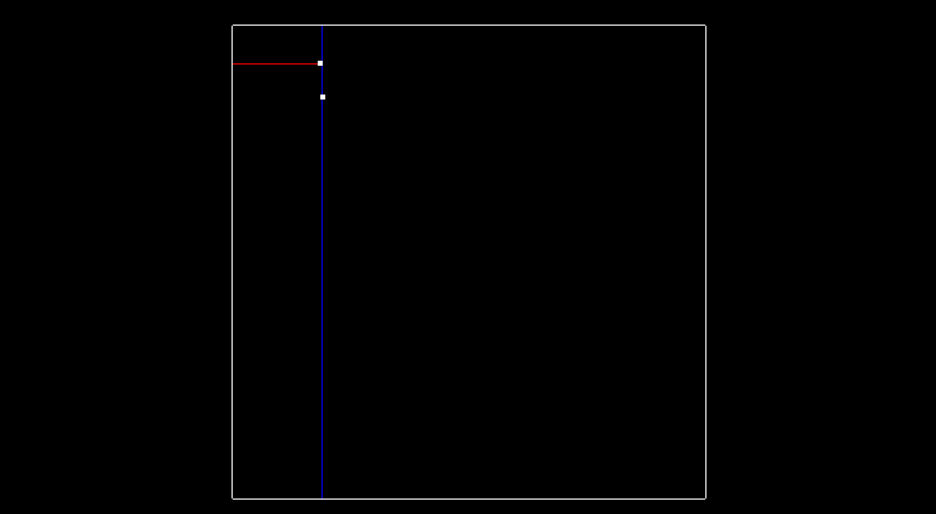
The next point is (-6.3, 8.4). Since we previously split in the x-dimension, and -6.3 is less than -6.2. This Node will be created and be a part of root's left node. The point (-6.3, 8.4) will split the region in the y dimension.
To recap, the root was at depth 0, and split the x region. The next point became the left child of root and had a depth of 1, and split the y region.
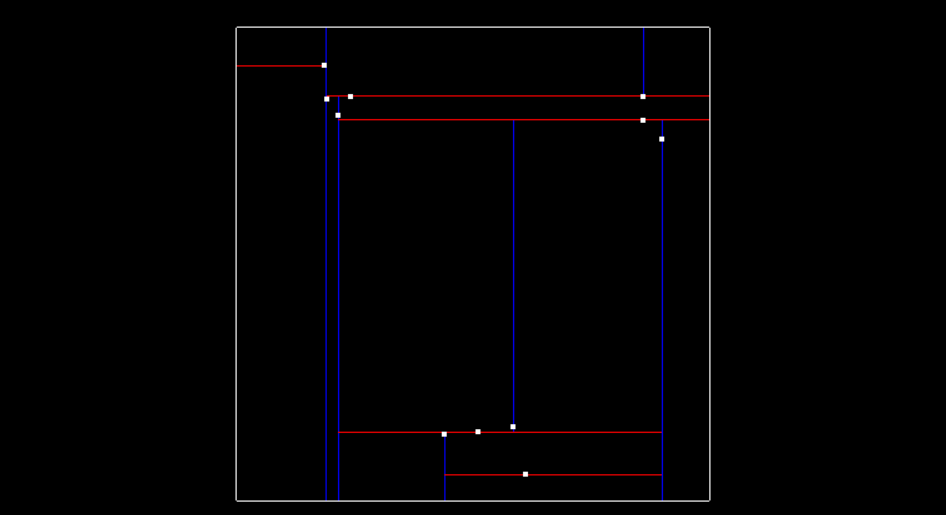
A point at depth 2 will split the x region again, so the split dimension number can actually be calculated as depth % 2, where 2 is the number of dimensions we are working with. The image below shows how the tree looks after inserting the second point.
Then here is what the tree looks like after inserting two more points (-5.2, 7.1) and (-5.7, 6.3), and having another x split division from point (-5.7, 6.3). The tree is now at depth 2.
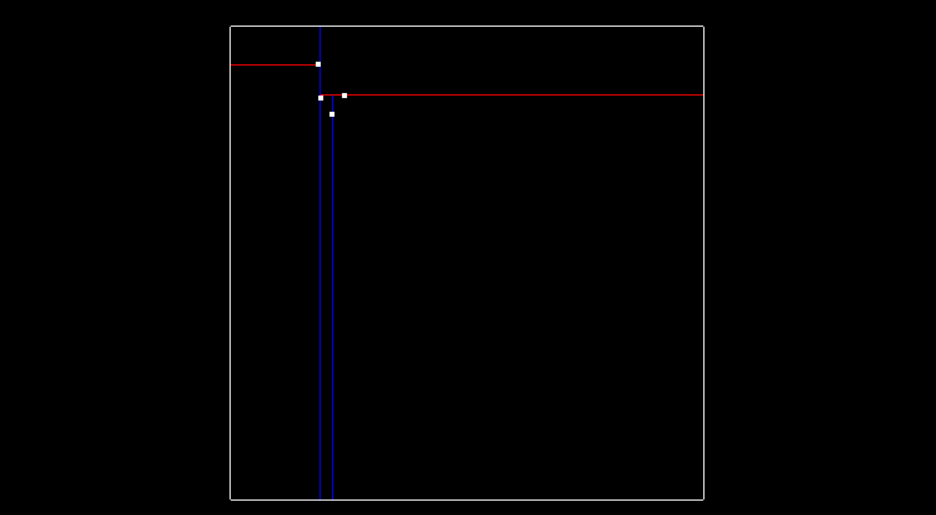
The image below shows so far what the tree looks like after inserting those 4 points. The labeled nodes A, B, C, D, and E are all NULL.
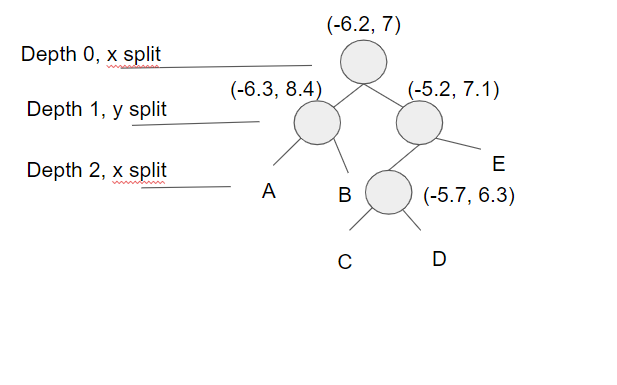
Answer
D
Improving the Tree
Having a balanced tree that evenly splits regions improves the search time for finding points later. To improve the tree, insert points that alternate between splitting the x region and the y region evenly. To do this pick the median of sorted x and y points. For instance if you are inserting the first four points that we used above (-6.3, 8.4), (-6.2, 7), (-5.2, 7.1), (-5.7, 6.3) we would first insert (-5.2,7.1) since it is the median along the x axis. If there is an even number of elements the lower median is chosen. The next point to be inserted would be (-6.2, 7), the median of the three points for y. This would be followed by (-5.7,6.3) the lower median between the two for x, and then finally (-6.3,8.4). This ordering will allow the tree to more evenly split the region space and improve search time later.
Example of Insertion for Binary Tree
Implementing a recursive helper function to insert points can be a very nice way to update Nodes. The basic idea is that the tree is traversed until the Node it arrives at is NULL, in which case a new Node is created and replaces the NULL Node. For assigning a Node, one way is to use a double pointer. You could pass in a pointer to the node, starting at root, and then when you want to replace a node you can dereference the double pointer and assign it to the newly created Node. Another way of achieving this is by using a pointer reference as well.
Double Pointer
void insert(BinaryTreeNode **node, int data)
{
if(*node == NULL)
{
*node = getNewNode(data);
}
else if(data < (*node)->data)
{
insert(&(*node)->left, data);
}
else
{
insert(&(*node)->right, data);
}
}Pointer Reference
void insert(BinaryTreeNode *&node, int data)
{
if(node == NULL)
{
node = getNewNode(data);
}
else if(data < node->data)
{
insert(node->left, data);
}
else
{
insert(node->right, data);
}
}Searching Points in a KD-Tree
- Once points are able to be inserted into the tree, the next step is being able to search for nearby points inside the tree compared to a given target point. Points within a distance of
distanceTolare considered to be nearby. The KD-Tree is able to split regions and allows certain regions to be completely ruled out, speeding up the process of finding nearby neighbors.
- The naive approach of finding nearby neighbors is to go through every single point in the tree and compare their distances with the target, selecting point indices that fall within the distance tolerance of the target. Instead with the KD-Tree you can compare distance within a boxed square that is
2 x distanceTolfor length, centered around the target point. If the current node point is within this box then you can directly calculate the distance and see if the point id should be added to the list of nearby ids. Then you see if your box crosses over the node division region and if it does compare that next node. You do this recursively, with the advantage being that if the box region is not inside some division region you completely skip that branch.
Euclidean Clustering
- Now, it is time to find clusters in our point data.
Once the KD-Tree method for searching for nearby points is implemented, its not difficult to implement a euclidean clustering method that groups individual cluster indices based on their proximity. Inside
cluster.cppthere is a function calledeuclideanClusterwhich returns a vector of vector ints, this is the list of cluster indices.
- To perform the clustering, iterate through each point in the cloud and keep track of which points have been processed already. For each point add it to a list of points defined as a cluster, then get a list of all the points in close proximity to that point by using the search function from the previous exercise. For each point in close proximity that hasn't already been processed, add it to the cluster and repeat the process of calling proximity points. Once the recursion stops for the first cluster, create a new cluster and move through the point list, repeating the above process for the new cluster. Once all the points have been processed, there will be a certain number of clusters found, return as a list of clusters.
Pseudocode
Proximity(point,cluster):
mark point as processed
add point to cluster
nearby points = tree(point)
Iterate through each nearby point
If point has not been processed
Proximity(cluster)
EuclideanCluster():
list of clusters
Iterate through each point
If point has not been processed
Create cluster
Proximity(point, cluster)
cluster add clusters
return clusters