Estimating TTC with a Camera

It is really hard to measure metric distance with a camera. What you get from a camera is a 2D image, and you can't really tell how large or far away objects are without making some various simplifying assumptions. You could say for example that all vehicles have a width of 1.7 meters and the road surface is always flat in level. These assumptions are never true in real life. 🤢

Measuring TTC without distance

Monocular cameras are not able to measure metric distances. They are passive sensors that rely on the ambient light which reflects off of objects into the camera lens. It is thus not possible to measure the runtime of light as with Lidar technology.

To measure distance, a second camera would be needed. Given two images taken by two carefully aligned cameras (also called a stereo setup) at the same time instant, one would have to locate common points of interest in both images (e.g. the tail lights of the preceding vehicle) and then triangulate their distance using camera geometry and perspective projection. For many years, automotive researchers have developed stereo cameras for the use in ADAS products and some of those have made it to market. Especially Mercedes-Benz has pioneered this technology and extensive information can be found here : http://www.6d-vision.com/.

With more advanced ADAS products and with autonomous vehicles however, stereo cameras have started to disappear from the market due to their package size, the high price and the high computational load for finding corresponding features.

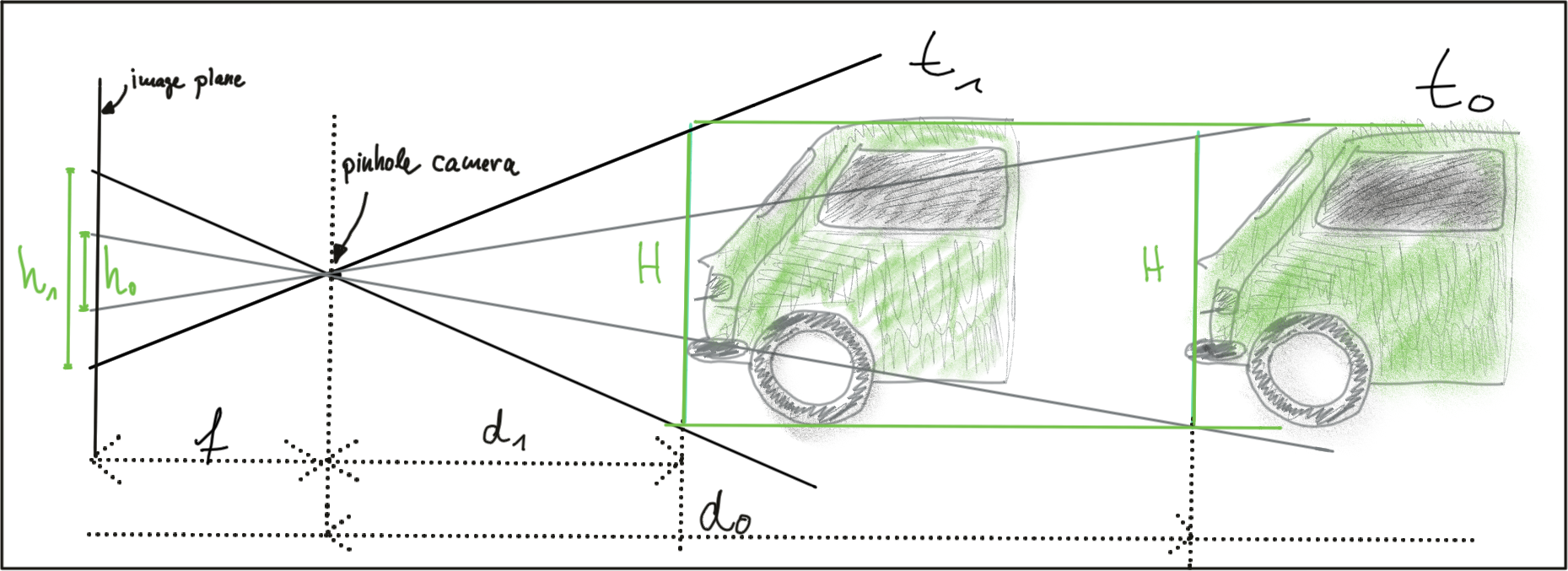
Let us take a look at the following set of equations:

The Problem with Bounding Box Detection

In the figure below, a neural network has been used to locate vehicles in successive images of a monocular camera. For each vehicle, the network returns a bounding box, whose width and/or height could in principal be used to compute the height ratio in the TTC equation.

When observed closely however, it can be seen that the bounding boxes do not always reflect the true vehicle dimensions and the aspect ratio differs between images. Using bounding box height or width for TTC computation would thus lead to significant estimation errors.

In most engineering tasks, relying on a single measurement or property is not reliable enough. This holds especially true for safety-related products. Therefore, we want to consider whether there are further properties of vehicles and objects we can observe in an image.

Using Texture Key-points Instead

Instead of relying on the detection of the vehicle as a whole we now want to analyze its structure on a smaller scale. If were possible to locate uniquely identifiable key-points that could be tracked from one frame to the next, we could use the distance between all key-points on the vehicle relative to each other to compute a robust estimate of the height ratio in out TTC equation. The following figure illustrates the concept.

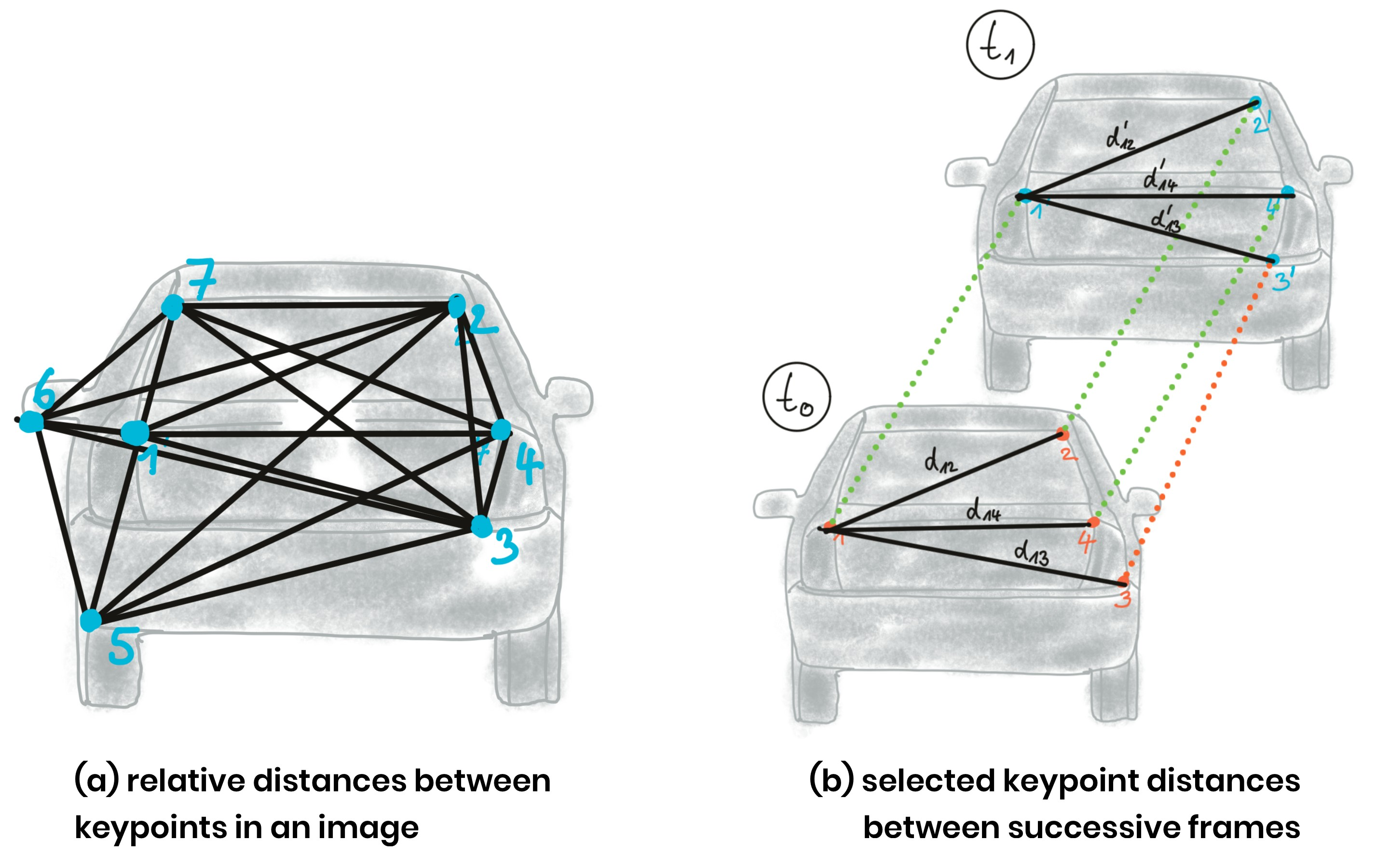
Computing TTC from Relative Keypoint Distances

Measuring TTC is a 4 Step Process

1. A bounding box is needed around the preceding vehicle that enables us to focus properly on the relevant object in the image.

2. A set of key points is necessary for every image that arise from the camera.

3. We need to match key points between successive frames to establish correspondences.

4. We look at relative distances between correspondences within the bounding box and compute a stable estimate of TTC.

Imagine a set of associated key-point between two successive frames which contain a large number of mismatches. Computing the mean distance ratio as in the function we just discussed would presumably lead to a faulty calculation of the TTC. A more robust way of computing the average of a dataset with outliers is to use the median instead.